Гармонические колебания вселенной (Часть 5)
Решающие успехи — это периоды обобщений.
Явления, казавшиеся разобщёнными,
становятся разными аспектами
одного и того же процесса
Р. Фейнман
До 1970-х — 80-х годов стабильные ритмы природы часто назывались по именам их открывателей, например, циклы солнечной активности Вольфа, Хейла, орбитальные периоды Миланковича, климатический цикл Брикнера смены теплых и сухих лет холодными и влажными годами. Среднее значение этого цикла было равно 35 годам, но сам период менялся от 25 до 50 лет.
Исследователи писали о ритмах с периодами 50-80, 80-110 и более лет. Низкая точность определения большинства периодов и отсутствие их классификации свидетельствовали о самой начальной стадии понимания причин и следствий существования стабильных гармонических колебаний природы.
5.1. Гармония земных ритмов и их классификация
Сложное именуется красивым, если
его части гармоничны в сочетании.
Пифагорейцы
Для изучения стабильных гармоник климата использовались ряды годовых приростов деревьев и метод Фурье для определения периодов и амплитуд основных гармонических составляющих природных процессов. На границе леса и тундры в сухих местах обитания деревья чувствительны к изменению среднегодовых температур воздуха и работают почти как самописцы измерительных приборов. Гармонические колебания были выделены также из рядов наблюдений за солнечной и сейсмической активностью. Суммы основных найденных ритмов являются эмпирическими моделями природных процессов, которые позволяют восстанавливать прошлое и прогнозировать будущее (рис. 5.1).
Сначала автор классифицировал полученные и известные ранее природные (N) периоды ТN с помощью октав из 4-х нот, начальным членом которой был выбран сидерический период обращения Луны Т0 [Берри и др., 1979]:
ТN = Т 0*2 N /n = 27, 32*2 N /4 суток = 0,075*2N/4 лет (5.1)
где N — последовательность целых чисел; n = 4 — количество нот в октаве. Главная последовательность найденных гармоник (5.1) связывалась с периодическими воздействиями Солнца и Луны на Землю и приливных планет (Меркурий, Венера, Земля и Юпитер) на активность Солнца.
Затем из менее энергетических ритмов была выделена дополнительная прогрессия (P) гармонических колебаний. Она соответствовала воздействиям орбитальных движений Юпитера, Сатурна, Урана и Нептуна, которые изменяют положение центра тяжести СС (барицентра) и все моменты движения небесных тел, включая Солнце [Берри, 1987, Berry, 1991]:
TС = 0.082*2С/4 лет (5.2)
Прогрессии (5.1, 5.2) были объединены в одну с октавой из 16-нот [Берри, 1987]:
TК = Т 0*2К/N = 0.075*2К/16 лет (5.3)
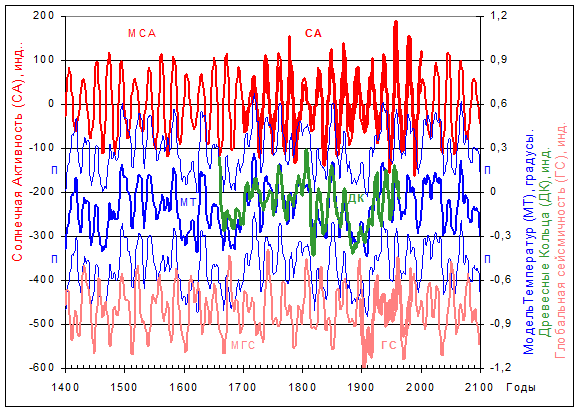
Рис. 5.1. Данные прироста древесных колец (ДК), солнечной активности (СА) и глобальной сейсмической (ГС) (индексы) и гармонические модели годовых температур (МТ) воздуха с коридором её погрешностей (П), солнечной активности (МСА) и глобальной сейсмичности (МГС). Максимумы ГС направлены вниз для удобства сопоставления графиков
Иллюстрация: Берри, 2006, Berry, 2006.
Вопрос о выборе периода (гармоники) Луны в качестве начального члена прогрессии (Т0) не обсуждается: Луна — наиболее изученный и влиятельный генератор земных колебаний [Максимов, 1970; Авсюк, 1996].
5.2. Лунные октавы астрономических периодов
Повторения во Вселенной стали
сводящим с ума заклинанием,
и я начал понимать, в чём дело.
Г. Честертон
Найденные классификации природных и астрономических периодов [Берри, 1987] свидетельствуют о существовании взаимосвязей между природными процессами разных маштабов, которые приводят к гармоничесским закономерностям распределения периодов. Гелиогеофизические, биологические, экономические, политические и другие колебательные процессы имеют общее внешнее происхождение [Берри, 1992, Berry, 1993]. Такой механизм объясняет совпадения периодов некоторых независимых земных процессов, например, колебаний годовых полушарных температур воздуха и показателей глобальной [Берри, 1991] и региональной [Berry, 2006] сейсмичности (рис. 5.1).
Поэтому закономерности земных и солнечных колебаний и причины их возникновения надо изучать, как классиков, по первоисточникам: периодам обращения и вращения небесных тел Солнечной системы (СС) [Берри, 1987, 1991, 1993, 2006, 2010; Berry, 1998, 2006, 2011]. Гармонические периоды формируются внутри СС при гравитационном взаимодействии небесных тел [Молчанов, 1966].
5.3. Лунные октавы из 16 нот в периодах обращения тел СС
Мелодии, которые мы слышим, прекрасны, но
неслыханно прекрасней то, что мы не слышим.
Джон Китс. Ода греческой урне.
Орбитальные гармонические движения тяжелых планет периодически перемещают барицентр СС относительно центра тяжести Солнца, изменяя одновременно моменты инерции Солнца, всех небесных тел и скорости их движений [Хлыстов и др., 1992]. Приливные планеты также изменяют форму нашей звезды и ее активность.
На земные процессы дополнительно влияют гармонические изменения солнечной активности (СА), приливные силы Луны (рис. 5.2) и Солнца, которые изменяют моменты и скорости вращения Земли. Гравитационные силы деформируют фигуру Земли (геоид), смещая твердое земное ядро относительно центра жидкого ядра, изменяя положения оси и величины скоростей вращения Земли [Берри, 1993; Авсюк, 1996; Сидоренков, 2002].
Длительные приливные и моментные взаимодействия небесных тел СС привели к почти целочисленным соизмеримостям (резонансам) в периодах их обращения и вращения. Равенство между периодами орбитального обращения и вращения Луны представляет собой характерный пример орбитально-спинового резонанса при отношении периодов 1:1. Соизмеримости (гармонические соотношения) орбитальных периодов наблюдаются у Плутона и Нептуна (2:3), Юпитера и Сатурна (2:5), трех галилеевых спутников Юпитера (1:2:4) и других небесных тел [Маров, 1981]. Точность резонанса планетарных систем Солнца и Юпитера или целочисленных соотношений периодов определяется отношением масс планет к массе Солнца или отношением масс спутников Юпитера к его массе (10–3) [Молчанов, 1966]. Эта же величина ограничивает точность приведенных ниже расчетов.

Рис. 5.2. Луну небес не приравнять к луне, что нарисована на полотне. Х. Ширвани.
Фото: Victor Habbick/freedigitalphotos.net
Для классификации и систематизации найденных природных гармоник автор много лет использовал прогрессии (5.1-5.3) с 4, 8 и 16 нотами в октаве с начальным членом (Т0), равным времени обращения Луны [Берри и др., 1979; Берри, 1987, 1992; Berry, 1991]. В 1998 г впервые было показано, что 16-нотная лунная октава (5.3), используемая для классификации гелиогеофизических ритмов, является закономерностью распределения резонансных периодов СС. Из анализа 23-х периодов обращения небесных тел планетарных систем Солнца, Юпитера и периода Луны (табл. 5.1) получена гармоническая закономерность (5.3), статистическая достоверность которой составила 96% [Berry, 1998].
Анализируемые гармонические периоды заполняют в табл. 5.1 только 11 позиций прогрессии (5.3), или примерно 69 % частот 16-нотной октавы СС. Незаполненные 5 нот (7, 8, 10, 15, 16) являются прогнозными периодами закономерности (5.3). Верность прогнозов подтверждена в табл. 5.2 и 5.3.
Таблица 5.1. Сопоставление величин TK (5.3), периодов обращения Луны, планет и спутников Юпитера (ТПС); значения показаны в годах и днях.
|
N |
Октавы |
К |
TK(г, д) |
TПС (г, д) |
SYMBOL 68 \f "Symbol"T% |
Планеты и спутники |
|
1 |
0 |
0 |
27,32 д |
27,32 |
0 |
Луна |
|
2 |
3 |
49 |
0,625 |
0,615 |
-1,6 |
Венера |
|
2 |
-4 |
-63 |
1,786 д |
1,769 |
-0,952 |
I Ио |
|
2 |
-3 |
-47 |
3,561 д |
3,551 |
-0,281 |
II Европа |
|
2 |
-2 |
-31 |
7,13 д |
7,155 |
0,351 |
III Ганимед |
|
3 |
10 |
162 |
83,53 |
84,01 |
0,575 |
Уран |
|
3 |
11 |
178 |
167,1 |
164,8 |
-1,376 |
Нептун |
|
3 |
3 |
50 |
238,4 д |
240 |
0,671 |
XIII Леда |
|
4 |
-6 |
-93 |
0,486 д |
0,489 |
0,617 |
V Амалтея |
|
4 |
3 |
51 |
248,9 д |
250,6 |
0,683 |
VI Гималия |
|
5 |
3 |
52 |
260 д |
260 |
0 |
X Лиситея |
|
5 |
3 |
52 |
260 д |
260,1 |
0,038 |
VII Элара |
|
6 |
7 |
117 |
11,89 |
11,86 |
-0,252 |
Юпитер |
|
6 |
-1 |
-11 |
16,96 д |
16,689 |
-1,598 |
IV Каллисто |
|
9 |
4 |
72 |
618 д |
617 |
-0,162 |
XII Ананке |
|
11 |
4 |
74 |
1,846 |
1,880 |
1,842 |
Марс |
|
11 |
8 |
138 |
29,55 |
29,46 |
-0,305 |
Сатурн |
|
12 |
11 |
187 |
246,7 |
247,7 |
0,405 |
Плутон |
|
12 |
1 |
27 |
0,2414 |
0,241 |
-0,166 |
Меркурий |
|
12 |
4 |
75 |
703,8 д |
692 |
-1,677 |
XI Карме |
|
13 |
3 |
60 |
1,006 |
1 |
-0,596 |
Земля |
|
13 |
4 |
76 |
735 д |
735 |
0 |
VIII Пасифе |
|
14 |
4 |
77 |
767,5 д |
758 |
-1,238 |
IX Синопе |
|
σn-1= |
0,880 |
Взаимодействия тел СС создают гелиогеофизические и биофизические колебания, наблюдаемые в природе и обществе [Берри, 1992, Berry, 1993]. Именно существование этой астрономической закономерности (5.3) позволяло находить, объединять и классифицировать земные ритмы разной физико-биологической природы. Стало понятно, что найденные классификации являются следствием гармонического распределения периодов, формируемой внутри СС.
Как и к любой другой эмпирической закономерности здесь возникают следующие вопросы:
1. Можно ли расширить временные границы закономерности (5.3) за пределы периодов (0,5 суток –250 лет) обращения небесных тел СС?
2. Можно ли уточнить обнаруженную гармоническую закономерность и увязать её возникновение с физическими процессами, законами и константами?
5.4. Лунные октавы из 16 нот в орбитальных движениях планет СС и в земных процессах
Луна волнует море, как женщину.
Эрнест Хемингуэй

Иллюстрация: lrargerich/flickr.com
По соотношению легких и тяжелых изотопов водорода (H) и кислорода (O) в годовых слоях покровных ледников Антарктиды и Гренландии можно судить о гармонических изменениях глобальной температуре приземного слоя воздуха. В эпохи похолодания легкие изотопы химических элементов воды (Н2О) из экваториального пояса в большем количестве вместе с парами переносятся к полярным ледникам. Чем больше разница температур воздуха между экваториальным поясом и полюсами, тем больше легких изотопов переносится к полярным льдам. А в периоды потепления при таянии полярных ледников легкие изотопы возвращаются в мировой океан. Поэтому послойный изотопный анализ льда полярных ледников позволяет судить о прошлых гармонических изменениях климата (рис. 5.4). Аналогичные климатические исследования можно проводить, изучая слои донных осадков океанов. Количество легких изотопов в отложениях океанов увеличивается в теплые периоды.
Впервые такая палеоклиматическая реконструкция для 700 тыс лет была проведена Эмилиани по донным осадкам раковин фораминифер в 1950-х годах. По этим данным температуры поверхности Карибского моря снижались в ледниковые эпохи на 6 ᵒС. К концу 1960-х годов Имбри и Кипп с помощью многофакторного анализа показали, что основная часть изменений изотопного состава морской воды связана с изменениями объемов ледниковых покровов, так как легкие изотопы испаряются и концентрируются в ледниках. Реальные и прогнозные гармонические колебания температур поверхностного слоя воды колебались в пределах 2 ᵒС [Берри, 1992], что мы и наблюдаем на реконструкции рис. 5.4, полученной из Антарктической скважины.

Рис. 5.4. Глобальные температуры за последние 420 тыс лет, восстановленные по данным бурения льда Антарктиды на станции Восток [Petit et al. 2001], созданной в декабре 1957 г. Реконструкция содержит четыре ледниковых и пять межледниковых (красных) периодов, включая современное потепление (красный прямоугольник). Пунктирная линия показывает современную температуру.
В табл. 5.2 гармонические колебания лунной прогрессии (5.3) сопоставлены с астрономическими периодами (TА) орбитальных характеристик планет СС [Куликов и Сидоренков, 1977, Монин, 1982, Brouwer, Woerkom, 1950], а также с периодами земных (TЗ) эколого-геофизических колебаний. Последние выделены из временных рядов содержания тяжелого изотопа кислорода в донных осадках океанов за последние 0,7 млн лет [Hays et al., 1976, Берри, 1992, Зубаков, 1990, Raymo, 1992] и из рядов прироста деревьев [Берри, 2006].
Астрономические и земные гармоники хорошо соответствуют друг другу и совпадают с членами прогрессии TK (5.3) [Berry, 1998]. Например, ноте N = 4 в октаве 18 (табл. 5.2) соответствует астрономический период в 22,4 тыс лет [Монин, 1982], а в октаве 20 — эколого-геофизический период, равный средней длине последних оледенений в 90 тыс лет [Raymo, 1992]. Эти периоды отличаются друг от друга в 4 раза. Астрономические циклы являются первичными, а их гармоники земных процессов — вторичными колебаниями.
Таблица 5.2. Сопоставление земных периодов (TЗ) и периодов СС (TСС) с членами прогрессии TK (5.3), периоды даны в тысячах лет
|
N |
K |
Октава |
TK |
TЗ/TА |
SYMBOL 68 \f "Symbol"T% |
Периоды изменений |
|
1 |
320 |
20 |
78,43 |
79 |
0,73 |
Экологических условий |
|
2 |
305 |
19 |
40,95 |
40,9 |
-0,12 |
Наклона земной орбиты |
|
3 |
306 |
19 |
42,76 |
43 |
0,56 |
Экологических условий |
|
4 |
291 |
18 |
22,33 |
22,4 |
0,31 |
Перигелия орбиты Земли |
|
4 |
323 |
20 |
89,32 |
90 |
0,76 |
Климатических условий |
|
5 |
308 |
19 |
46,60 |
47 |
0,86 |
Перигелия Сатурна |
|
5 |
324 |
20 |
93,27 |
93 |
-0,29 |
Экологических условий |
|
6 |
293 |
18 |
24,35 |
24 |
-1,44 |
Климатических условий |
|
6 |
325 |
20 |
97,40 |
96 |
-1,44 |
Климатических условий |
|
7 |
294 |
18 |
25,43 |
25,73 |
1,18 |
Положения полюса Земли |
|
8 |
359 |
22 |
424,9 |
425 |
0,03 |
Геологических условий |
|
9 |
312 |
19 |
55,46 |
56 |
0,97 |
Экологических условий |
|
9 |
344 |
21 |
221,80 |
220 |
-0,81 |
Перигелия Меркурия |
|
10 |
297 |
18 |
28,96 |
28,6 |
-1,24 |
Наклона земной орбиты |
|
11 |
330 |
20 |
121,00 |
121 |
-0,03 |
Экологических условий |
|
11 |
330 |
20 |
121,00 |
121,6 |
0,50 |
Эксцентриситета земной орбиты |
|
11 |
394 |
24 |
1935,00 |
1923 |
-0,62 |
Эксцентриситета земной орбиты |
|
12 |
395 |
24 |
2021,00 |
2000 |
-1,04 |
Перигелия Нептуна |
|
13 |
220 |
13 |
1,03 |
1,029 |
0,10 |
Экологических условий |
|
13 |
300 |
18 |
32,98 |
33 |
0,06 |
Экологических условий |
|
14 |
317 |
19 |
68,87 |
68 |
-1,26 |
Климатических условий |
|
15 |
270 |
16 |
8,99 |
9 |
0,11 |
Климатических условий |
|
15 |
318 |
19 |
71,92 |
72 |
0,11 |
Перигелия Марса |
|
16 |
287 |
17 |
18,78 |
18,9 |
0,64 |
Перигелия Земли |
|
16 |
351 |
21 |
300,40 |
300 |
-0,13 |
Перигелия Юпитера |
|
sn-1 = |
0,785 |
В табл. 5.2 показаны совпадения периодов гармонической лунной прогрессии (5.3) с 14-ю эколого -геофизическими циклами Земли (TЗ) и с 11-ю астрономическими периодами (TА) изменения планетарных орбит. Эти совпадения с вероятностью 99% не являются случайными. Из табл. 5.2, видно, что стабильные колебания природных процессов с периодами до 2 млн лет (нота N = 12, октава О = 24) возникают в пределах СС [Brouwer, Woerkom, 1950].
5.5. Лунные октавы из 16 нот в геологических периодах и в движении СС вокруг центра Галактики
Все возвращается на круги своя
Ниже в табл. 5.3 дано сравнение гармоник лунной прогрессии (5.3) и ритмов пересечения СС двух галактических рукавов (ветви Ориона-Лебедя и ветви Киля-Стрельца) при ее орбитальном движении вокруг центра нашей Галактики [Berry, 1998]. Рукава (ветви) — это струйные потоки вещества, плотность которых убывает по мере удаления от центра Галактики (рис. 5.5). Они представлены пылевыми облаками, кометами и молодыми звездами. При пересечении рукава в перигалактии орбиты (ближайшей точке орбиты к центру Галактики) СС взаимодействует с повышенной плотностью вещества в галактическом потоке (рис. 5.6). В эти периоды на Земле формируются очень четкие геологические границы галактических годов (периодов обращения СС вокруг центра Галактики) из-за более частых столкновений Земли с галактическими кометами, что приводит к значительным вымираниям разных видов растительного и животного мира (рис. 5.7), особенно 500 и 250 млн лет назад [Баренбаум, 1991, 2010, Берри, 1993].

Рис. 5.5. Элементы Галактики Млечного Пути. На фото другой галактики, подобной нашей, нанесены названия рукавов (ветвей) Галактики Млечного Пути.
Фото: astrogalaxy.ru

Рис. 5.6. Галактические годы Солнечной системы (K = 1 – 14, кружки на графике) и их геологические границы в миллиардах лет. Римскими цифрами обозначены геологические эоны: I — Фанерозой, II, III, IV - Верхний, Средний и Нижний Рифей, V — Карелий, VI — Архей. Разрывы на прямой, происходившие 1,1, 1,65 и 2,6 млрд лет назад, соответствуют временам пролета звезд галактических потоков вблизи Солнца
Иллюстрация: Берри, 1992; Berry, 1993

Рис. 5.7. Восстановленная по ископаемым остаткам интенсивность вымирания в % биологических родов в разные геологические периоды Фанерозоя (см. рис. 5.5). На горизонтальных осях показаны время, в млн лет тому назад, и геологические периоды: Неоген (Neogen, N), Палеоген (Pg), Мел (Cretaceous, K), Юра (Jurassic, J) Триас (Triassic, Tr), Пермь (Permian, P), Карбон (Carboniferous, C ), Девон (Devonian, D), Сирур (Silurian, S), Ордовик (Ordovician, O), Кембрий (Cambrian, Cm).
Иллюстрация: Dragons flight/en.wikipedia.org
Таблица 5.3 . Сопоставление величин ТK (5.3 ) [Berry, 1998] и геологических периодов (ТGБ) А. А. Баренбаума [1991]. Время показано в млн лет.
|
N |
K |
ТK |
ТGБ |
ΔT % |
Геологические периоды |
|
1 |
448 |
20,1 |
20 |
0,50 |
Неоген, Триас, Ордовик |
|
2 |
449 |
21,0 |
21 |
0,00 |
Палеоцен, Пермь, Кембрий |
|
3 |
450 |
21,9 |
22 |
-0,46 |
Карбон, Кембрий |
|
4 |
451 |
22,9 |
23 |
-0,44 |
Палеоцен |
|
5 |
452 |
23,9 |
24 |
-0,42 |
Мел |
|
6 |
453 |
24,9 |
25 |
-0,40 |
Карбон, Венд |
|
7 |
454 |
26,0 |
- |
- |
- |
|
8 |
455 |
27,2 |
27 |
0,74 |
Триас, Ордовик |
|
9 |
456 |
28,4 |
28 |
1,41 |
Мел, Девон, Венд |
|
10 |
457 |
29,6 |
- |
- |
- |
|
11 |
506 |
247,8 |
250 |
-0,89 |
Период обращ. СС (Галактический год) |
|
12 |
459 |
32,3 |
32 |
0,93 |
Мел, Девон, Венд |
|
13 |
460 |
33,8 |
- |
- |
- |
|
14 |
461 |
35,3 |
- |
- |
- |
|
15 |
462 |
36,8 |
37 |
-0,54 |
Юра, Силур, Верхний Рифей |
|
16 |
447 |
19,2 |
19 |
1,04 |
Пермь, Кембрий |
|
σn-1= |
0,7340 |
При значении стандартного отклонения σn-1= 0,7340, гармоническая закономерность ТK (5.3) существует в распределении 26-ти геологических периодов ТGБ (табл. 5.3) с вероятностью 99 % в соответствии с критерием Фишера [Berry, 1998]. Прогрессия (5.3) используется для описания ритмов природы, точность определения которых относительно мала. Например, геологические периоды табл. 5.3 определяются всего двумя знаками.
Оказалось, что гармоническая закономерность, полученная в диапазоне периодов 0,3 суток — 250 лет (табл. 5.1), сохранила свою работоспособность до периода в 250 млн лет (табл. 5.3). Столь широкий диапазон (3*1011) эмпирической зависимости свидетельствует о существовании взаимосвязанных физических процессов, приводящих к гармонии природных колебаний и на астрономическом уровне.
Читайте также:
Гармонические колебания Вселенной (Часть 1)
Гармонические колебания Вселенной (Часть 2)
Гармонические колебания Вселенной (часть 3)
Гармонические колебания вселенной (Часть 4)
Гармонические колебания Вселенной (Часть 6)
Борис Берри. Специально для Великой Эпохи