Китайські фізики придумали і реалізували квантовий варіант настільної гри в го

Вони показали, що безліч можливих позицій в такій грі значно більше, ніж у класичного аналога. Вони показали, що безліч можливих позицій в такій грі значно більше, ніж у класичного аналога.Завдяки своїй складності квантове го може стати одним із перспективних кандидатів для демонстрації квантової переваги. Стаття опублікована на arXiv.org.

У 2016 році програма AlphaGo, яка використовує алгоритми машинного навчання, обіграла Лі Седоля, а потім і Ке Цзе — найсильніших гравців у го. На той момент здавалося, що обробити таку величезну кількість інформації й обіграти професіонала просто неможливо.

Учені під керівництвом Сань Мінь Цзінь (Xian-Min Jin) з Науково-технічного університету Китаю вирішили збільшити й без того велике число можливих позицій гри за допомогою квантової механіки. Таке завдання стає цікавим не тільки з точки зору можливостей машинного навчання, але і з точки зору квантових технологій. Воно може бути дуже складним для класичного комп'ютера, що дає можливість квантовим обчисленням продемонструвати свою перевагу.

У класичне го грають камінням двох кольорів — чорним і білим. Два гравці по черзі виставляють камені на перетину клітин ігрового поля розміром 19 на 19 (можливі варіанти 9 на 9, 13 на 13). Мета гри — відгородити своїми каменями територію більшу, ніж у суперника. Додаткові очки можна отримати, якщо на захопленій території є камені супротивника.

Автори запропонували нову версію гри з використанням квантової суперпозиції й вимірювань. У квантовому го з'являється можливість ставити камінь відразу у два різних місця дошки. Гравець вибирає дві позиції, в яких може перебувати камінь і вказує їх. З цього моменту і до того, як цей камінь буде виміряно, він знаходиться в стані суперпозиції. Тобто з певними можливостями він може бути виявлений в одному або іншому положенні. Навіть гравець, який поставив цей квантовий камінь не знає, де саме виявиться камінь після вимірювання. Вимірювання у квантовій механіці змушує квантовий об'єкт вибрати один із двох станів (сколапсувати). В такому випадку після вимірювання квантовий камінь перетворюється в класичний і займає тільки одне місце на дошці. Вимірювання каменю відбувається тоді, коли на сусідньому перехресті з'являється інший камінь.

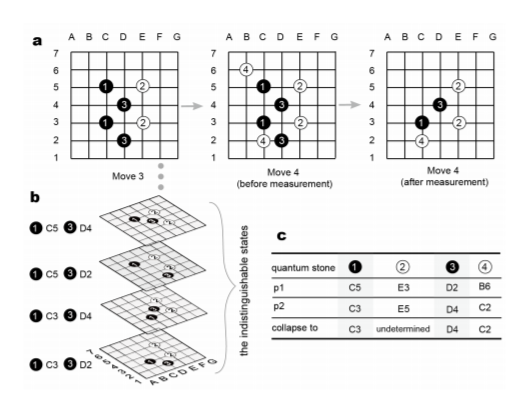
У початковому положенні на дошці знаходяться три квантових каменів: 1, 2, 3. На малюнку b показані всі варіанти, коли каміння 1 і 3 сколапсовані в одне з двох станів. Після постановки на дошку каменю 4, відбувається їх вимір каменів 1, 3 і вони стають класичними (права картинка).

Така варіація гри додає їй елемент випадковості й значно збільшує безліч можливого розставляння. Крім цього ускладнити гру можна й іншим способом: приховувати частину інформації про гру від учасників. У квантовому го можна дати гравцеві самому вибирати ймовірності положення каменю і не говорити про це супернику. У такому випадку гра може бути зведена до класичного го, якщо кожен раз одному з положень привласнювати одиничну ймовірність.

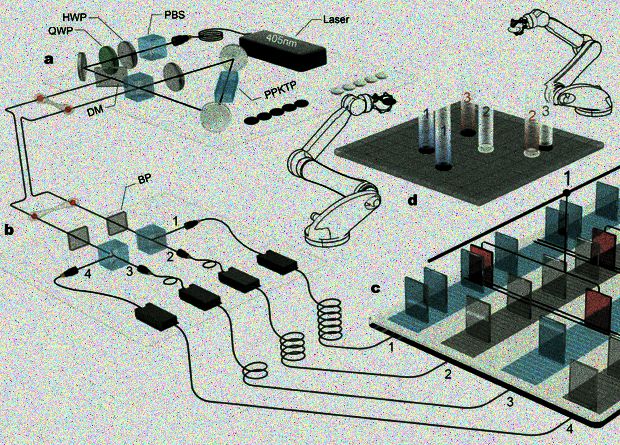
У дослідженні свого задуму автори пішли далі та створили експериментальний прототип гри. Для цього вони використовували джерело пар заплутаних фотонів, які вимірювалися за допомогою однофотонних детекторів. Кожен вимір у грі вироблявся надреальною квантовою системою, колапс якої говорить про те, куди необхідно поставити вимірюваний камінь. Така оптична схема дозволяє реалізовувати й варіант гри з прихованою інформацією.

Дерево з усіма можливими результатами гри на дошці 3 на 3 для (a) класичного го, (b) квантового го

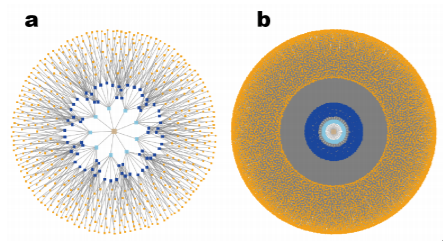
Найпростіша модель гри на дошці 3 на 3 показала, що безліч позицій для квантового го значно більша, ніж для класичного. Крім того, квантове го виявилося складнішим не тільки свого класичного аналога, але й інших недетермінованих ігор та ігор з прихованою інформацією. Завдяки своїй складності нова гра може стати полем для експериментів у галузі класичних і квантових алгоритмів.

Поки програми на основі алгоритмів машинного навчання показує успіхи в змаганні з людьми.